Arithmetic for Computers
1. BINARY ARITHMETIC
Always remember that:
- 0+0=0
- 1+0=1
- 1+1=10
- 1+1+1=11
For example 1010 + 01
1010
+ 01
______
1001
*1+1 carries us into the next column. In decimal form, 1+1=2. In binary, any digit higher than 1 puts us a column to the left (as would 10 in decimal notation). The decimal number "2" is written in binary notation as "10" (1*2^1)+(0*2^0). Record the 0 in the ones column, and carry the 1 to the twos column to get an answer of "10".
For example 1010 + 11
+1
1010
+ 11
______
1101
Work the columns right to left subtracting in each column. If you must subtract a one from a zero, you need to “borrow” from the left, just as in decimal subtraction.
For example: 1010110 − 101010 = 101100
| 0 | | 0 | | | | |
| ×1 | 10 | ×1 | 10 | 1 | 1 | 0 |
| − | | 1 | 0 | 1 | 0 | 1 | 0 |
| | 1 | 0 | 1 | 1 | 0 | 0 |
Multiplication in the binary system works the same way as in the decimal system:
101
* 11
____
101
1010
_____
1111
*Note that multiplying by two is extremely easy. To multiply by two, just add a 0 on the end.
Follow the same rules as in decimal division. For the sake of simplicity, throw away the remainder.
For Example: 111011/11
10011 r 10
_______
11)111011
-11
______
101
-11
______
101
11
______
10
2. HEXADECIMAL ARITHMETIC
- HEXADECIMAL NUMBER SYSTEM
Following are the characteristics of a hexadecimal number system.
- Uses 10 digits and 6 letters, 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F.
- Letters represents numbers starting from 10. A = 10, B = 11, C =12, D = 13, E = 14, F = 15.
- Also called base 16 number system.
- Each position in a hexadecimal number represents a 0 power of the base (16). Example − 160
- Last position in a hexadecimal number represents an x power of the base (16). Example − 16x where x represents the last position - 1.
Example:
Hexadecimal Number − 19FDE16
Calculating Decimal Equivalent −
| Step | Binary Number | Decimal Number |
|---|
| Step 1 | 19FDE16 | ((1 × 164) + (9 × 163) + (F × 162) + (D × 161) + (E × 160))10 |
| Step 2 | 19FDE16 | ((1 × 164) + (9 × 163) + (15 × 162) + (13 × 161) + (14 × 160))10 |
| Step 3 | 19FDE16 | (65536 + 36864 + 3840 + 208 + 14)10 |
| Step 4 | 19FDE16 | 10646210 |
Note − 19FDE16 is normally written as 19FDE.
Following hexadecimal addition table will help you greatly to handle Hexadecimal addition.
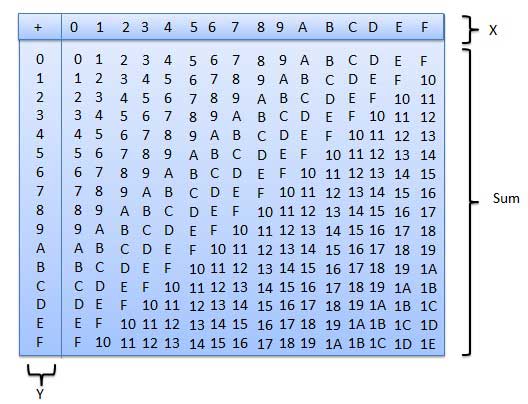
To use this table, simply follow the directions used in this example − Add A16and 516. Locate A in the X column then locate the 5 in the Y column. The point in 'sum' area where these two columns intersect is the sum of two numbers.
A16 + 516 = F16.
Example − Addition
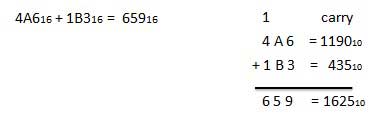
The subtraction of hexadecimal numbers follow the same rules as the subtraction of numbers in any other number system. The only variation is in borrowed number. In the decimal system, you borrow a group of 1010. In the binary system, you borrow a group of 210. In the hexadecimal system you borrow a group of 1610.
Example - Subtraction

 |
| 




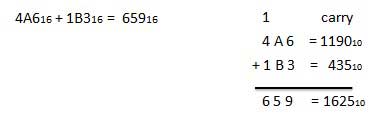

0 Comments:
Post a Comment